Scripting Examples

Table of Contents Index Glossary Op Index Parent

This is a child page. You can use Parent in the quick nav bar at the top or the bottom of the page to navigate directly back to the parent of this page. Some child pages are more than one level deep, and in that case will require more than one Parent click to reach the outermost document level.

§ 16.96.20 - Scripting Examples

Saturated Random Asterizations Script Results

§ 16.96.20.1 - Simple Random Asterizations

This script allows you to create asterizations in unpredictable colors all over the colorspace.

10 Z=ASTERIZE(rnd(0)*255,rnd(0)*255,rnd(0)*255,0,WID,0,ARMS,0,1,1)

§ 16.96.20.2 - Saturated Random Asterizations

This script creates only colors that exist around the outer edge of the color wheel; that is, they are always fully saturated colors.

REM lines 100-120 assign values for the asterize parameters we'll be changing
REM R, G and B are calculated as zero through one (you'll see why in a minute)
REM lines 130 through 150 locate the minimum R, G or B value
REM lines 160 through 180 move r g and b down so that the minimum value becomes zero
REM lines 190 through 210 locate the maximum R, G or B value
REM lines 220 through 240 scale R, G and B so that the maximum R, G or B value is 255
REM line 250 executes the asterize operation - with fully saturated random colors!
REM You can pass S out as the center saturation too, for fun

R=RND()*1: G=RND()*1: B=RND()*1: S=RND()*100
ARMS=(RND()*13)+4
WID = (RND()*20)+10

MI = R
IF G<MI THEN MI = G
IF B<MI THEN MI = B

R = R-MI
G = G-MI
B = B-MI

MA = R
IF G>MA THEN MA = G
IF B>MA THEN MA = B

R = (R/MA)*255
G = (G/MA)*255
B = (B/MA)*255

Z=ASTERIZE(R,G,B,0,WID,0,ARMS,0,1,1)
REM Z=ASTERIZE(R,G,B,S,WID,0,ARMS,0,1,1)

Custom Negative Operator Script Results

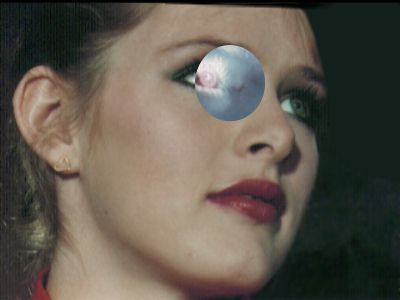
§ 16.96.20.3 - Image Negative Operator — Written entirely in the WIS scripting language

REM Demonstrates how to process an area selection - color negative function
X1=GETX1(0): Y1=GETY1(0): X2=GETX2(0): Y2=GETY2(0)
FOR Y=Y1 TO Y2
 A=PROGRESS(Y-Y1): IF A=1 THEN END
 FOR X=X1 TO X2
   R=255-GETRED(X,Y): G=255-GETGREEN(X,Y): B=255-GETBLUE(X,Y)
   A=PUTRED(X,Y,R): A=PUTGREEN(X,Y,G): A=PUTBLUE(X,Y,B)
 NEXT X
NEXT Y

If you look this script over, you'll see it is processing every pixel in a rectangle described by X1, Y1, X2 and Y2, values it retrieves from WinImages F/x. But in the example image, the effect is round; what's going on?

The answer is easy: When you make your area selection, F/x creates a mask that limits the application of changes to the selected area. Technically speaking, this means that although you process the entire rectangle that contains the area selection, F/x prevents your changes from being applied anywhere outside the actual selection shape, which is often not rectangular at all.

This very simple mechanism allows you to concentrate on figuring out more generally what you want to do to the image pixels, while F/x takes care of almost all the area selection issues for you; all you need to do with regard to area selections is process a rectangle exactly as we show you here.

Note:

If antialiasing and/or transparency is in use, then portions of the area selection will be "soft" in some places, and the pixel information you send to F/x will be mixed with the original image information according to how soft the area selection mask is.

You can (and should!) use the image negative example here to create other image operations.

Tip:

F/x does not use the mask to limit the pixel information you can read from the image, so you can write image processes that use pixel information outside the masked area to make computations.

Some scripts require access to an unchanged copy of the image in order to read information surrounding the pixel to be processed; if you fetch the surrounding pixels from the image you are changing, early changes affect later computations. Many filters are subject to this processing issue.

This task is easily addressed in the .WIS scripting language. When the user makes an area selection and the Scripting operator is the one in use, F/x will take a complete copy of the image and place it in the undo buffer before it calls your script. You can then use the GETREDU(), GETGREENU(), GETBLUEU() and GETALPHAU() functions to retrieve the original, unchanged image data from the undo buffer all during the time you are changing the actual image. Problem solved!

Here's a second example; this one uses the get and put hue functions to make the image greener. Otherwise, it is essentially the same as the negative example.

REM Demonstrates how to process an area selection - greener hue function
X1=GETX1(0): Y1=GETY1(0): X2=GETX2(0): Y2=GETY2(0)
FOR Y=Y1 TO Y2
 A=PROGRESS(Y-Y1): IF A=1 THEN END
 FOR X=X1 TO X2
   H=GETHUE(X,Y)+20
   A=PUTHUE(X,Y,H)
 NEXT X
NEXT Y

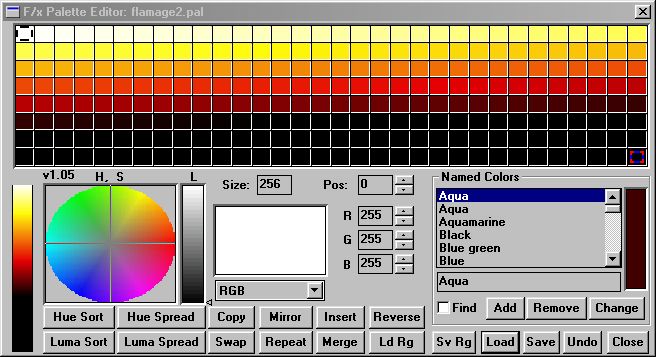
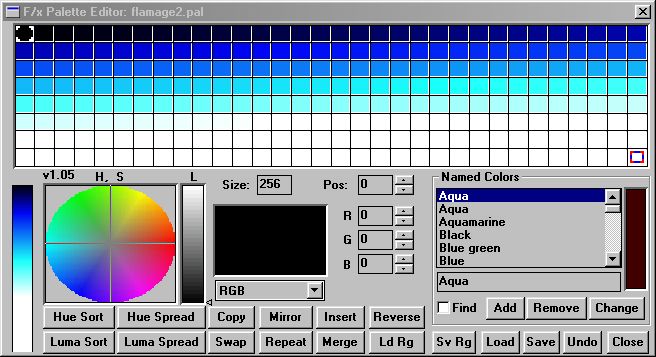
§ 16.96.20.4 - How to process a Palette

Bang palette, prior to inversion

Bang palette, inverted

REM This Inverts the BANG palette
A$ = "bang"
S = GETPALSIZE("BANG")-1
IF S > 0 THEN GOTO 170
PRINT "WHOOPS! ";A$;" HAS NO SIZE!"
END
FOR I=0 TO S
R=GETPALETTE(A$,I,"R")
G=GETPALETTE(A$,I,"G")
B=GETPALETTE(A$,I,"B")
R = 255-R
G = 255-G
B = 255-B
E=SETPALETTE(A$,I,"R",R)
E=SETPALETTE(A$,I,"G",G)
E=SETPALETTE(A$,I,"B",B)
NEXT I

or, more compactly...

§ 16.96.20.5 - How to process a Palette, reprised

REM This Inverts the BANG palette
A$ = "bang"
S = GETPALSIZE("BANG")-1
IF S > 0 THEN GOTO 170
PRINT "WHOOPS! ";A$;" HAS NO SIZE!"
END
FOR I=0 TO S
R=SETPALETTE(A$,I,"R",255-GETPALETTE(A$,I,"R"))
G=SETPALETTE(A$,I,"G",255-GETPALETTE(A$,I,"G"))
B=SETPALETTE(A$,I,"B",255-GETPALETTE(A$,I,"B"))
NEXT I

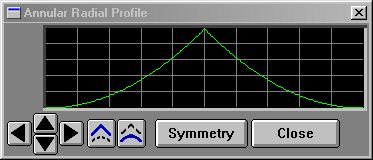
§ 16.96.20.6 - How to process a Profile

Annular Profile, prior to adding ten

Annular profile, with 10 added to every position

REM Adds 10 to the named profile curve
A$="annular"
for i=0 to 200
 d=getprof(A$,i)
 d = d + 10
 if d>255 then d=255
 e=setprof(A$,i,d)
next i

Multi-bolt Script Results

§ 16.96.20.7 - Multi-bolt Lightning Effect

This one is simple, but uses a little trick. You'll see that we're creating an angle that steps from 0 to 350; that accounts for the lightning bolt going across the selection at all angles. But we're passing in the angle (A) as the random number seed too — what that does is ensures that each bolt is different from the others. We don't go to 360, because rotationally speaking, 360 is the same as 0 and that means we'd shoot a bolt twice at the same place.

REM multi-bolt lightning effect
FOR A=0 TO 350 STEP 10
B=LIGHTNING(5,A,10,A,50,5,30,255,20,25,0,1)
NEXT A

§ 16.96.20.8 - Gold Foil

This script will create a gold foil texture.

r=128:g=128:b=128
a=colorfill(r,g,b):               REM basic middle grey to texturize
x=1:y=1:amt=100:luma=1
a=dither(x,y,amt,RND()*100,luma): REM make fine grain texture
x=8:y=8:amt=100
a=dither(x,y,amt,RND()*100,luma): REM add large grain to texture
radi=33
a=blur(radi):                     REM wear the edges off the texture
channel=5
a=minimum(channel,0):             REM expand the holes in the texture
amt=4
a=relief(amt):                    REM give it highlights and shadows
h=43:s=54:l=0:appsat=1
a=colorize(h,s,l,appsat):         REM turn it an aged gold color
amt=100:radi=20
a=sharpen(amt,radi)
x=3:y=3:amt=22
a=dither(x,y,amt,RND()*100,luma): REM give it some reflectivity
end

§ 16.96.20.9 - Camera Flare

Camera Flare Script Results

This is a great example of a more advanced script. This uses annular rings and an asterism to produce a very convincing "camera flare" effect. The effect follows a freehand area selection from the start point to the end point, and so can be made to track with bright spots and camera angles just as a real flare does - as shown in the example animation above.

REM this script creates a camera flare using annular ring and asterize
REM along with the freehand area selection tool (input from the user) and
REM a special elliptical area selection function. This doesn't set the
REM asterize profile because the default works well. For WinImages F/x R7.

REM general setup
a$="annular": REM this is the profile we'll need to change
pi = 3.141592653
xw = 30: REM xw and yw define the general size of the effects used
yw = 30
am = 1: REM am=1 means effects will be additive

REM get the endpoints of the line the user has drawn with the freehand tool
x1 = GETLI(0): y1 = GETLI(1): x2 = GETLI(2): y2 = GETLI(3)

REM p is the position along the line; siz is the size of the effect; peak is intensity

REM here are the mild rings
peak=50: gosub 6000: r = 255: g = 255: b = 255
p = 0.0: siz = 1.0: gosub 5000
p = .05: siz = .50: gosub 5000
p = .15: siz = .25: gosub 5000
p = .20: siz = .35: gosub 5000
p = .35: siz = .25: gosub 5000
p = .50: siz = .35: gosub 5000
p = .60: siz = .25: gosub 5000
p = .90: siz = .25: gosub 5000

REM here is the big flat glare
peak=25: gosub 7000: p=.75: siz=1.25: gosub 5000

REM here is the red ring
peak=50: gosub 8000: p=.75: g=0: b=0: siz=.90: gosub 5000

REM here is the little hotspot
peak=255: gosub 9000
p=.05: g=255: b=255: siz=.5: gosub 5000

REM asterize hot spot effect
cs=0: wid=20: rot=TLPOS(360): arms=7: p=.75: siz=2
x = x1 + ((x2-x1) * p): y = y1 + ((y2-y1) * p)
a=SELOVAL(x,y,xw*siz,yw*siz)
a=ASTERIZE(r,g,b,ccs,wid,rot,arms,1,0,am)

end

REM draws an annular ring at position p along the line in rgb and profile
x = x1 + ((x2-x1) * p): y = y1 + ((y2-y1) * p)
a=SELOVAL(x,y,xw*siz,yw*siz)
a=ANNULAR(r,g,b,0,am)
return

REM flat 75%, then hump to peak and back to zero profile subroutine
l=peak * .25
REM peak=200
for ii=0 to 150
a=SETPROF(a$,ii,l)
next ii
s=151: e=200
for ii=s to e
j=(ii-s)/(e-s)
k=abs(sin(j*pi))*peak
if j > .5 then goto 6120
if k < l then k=l
a=SETPROF(a$,ii,k)
next ii
return

REM flat,then fall-off profile subroutine
REM peak=64
s=150: e=200
for ii=0 to s-1
a=SETPROF(a$,ii,peak)
next ii
for ii=s to e
j = 1-((ii-s)/(e-s))
a=SETPROF(a$,ii,peak*j)
next ii
return

REM bright ring profile subroutine
s=150: e=200
REM peak=200
for ii=0 to s
a=SETPROF(a$,ii,0)
next ii
for ii=s to e
j=(ii-s)/(e-s)
k=abs(sin(pi*j))
a=SETPROF(a$,ii,k*peak)
next ii
return

REM burst profile subroutine
s=0: e=200
for ii=s to e
j=1-abs(sin(((ii/200)/2)*pi))
a=SETPROF(a$,ii,j*peak)
next ii
return

§ 16.96.20.10 - Setting Profiles via Scripting

The following examples will give you some "boilerplate" you can use in your own scripts.

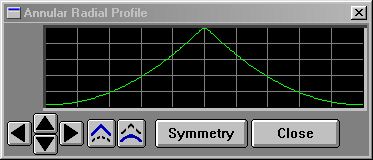
1/2 upwards curve

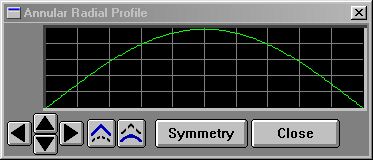p$ = "annular"
pi = 3.141592653979382
for i=0 to 200
j = i/200
v = sin(j*pi)*255
a = SETPROF(p$,i,v)
next i

You'll find the names for all the system profiles located here.

Full sinewave

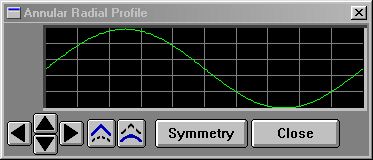p$ = "annular"
pi = 3.141592653979382
for i=0 to 200
j = (i/200)*2
v = ((1+sin(j*pi))/2)*255
a = SETPROF(p$,i,v)
next i

You'll find the names for all the system profiles located here.

Upwards Ramp

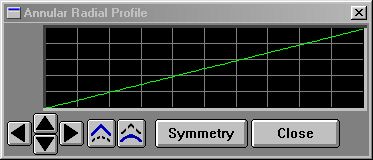p$ = "annular"
for i=0 to 200
j = (i/200)
v = j*255
a = SETPROF(p$,i,v)
next i

You'll find the names for all the system profiles located here.

Downwards Ramp

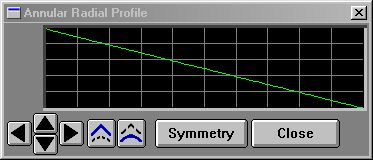p$ = "annular"
for i=0 to 200
j = (i/200)
v = (1-j)*255
a = SETPROF(p$,i,v)
next i

You'll find the names for all the system profiles located here.

Multiple Cycles of Sinewave (5)

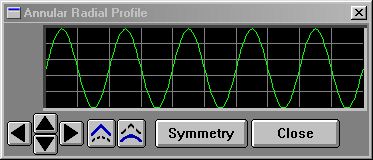p$ = "annular"
pi = 3.141592653979382
for i=0 to 200
j = (i/200)*2
v = ((1+sin(j*pi*5))/2)*255
a = SETPROF(p$,i,v)
next i

You'll find the names for all the system profiles located here.

Using STEP() to obtain square waves

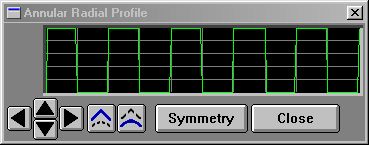p$ = "annular"
pi = 3.141592653979382
for i=0 to 200
j = (i/200)*2
v = STEP((1+sin(j*pi*5))/2,.5)*255
a = SETPROF(p$,i,v)
next i

This example feeds the portion of the sinewave formula that results in a sine wave of 0 to 1 to the STEP() function, with crossing parameter of .5. That produces a result of 0 below .5, 1 above .5.

You'll find the names for all the system profiles located here.

Using SMOOTHSTEP() to obtain squarish waves

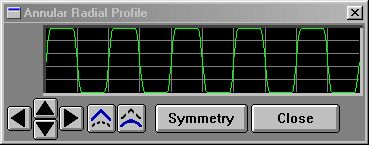p$ = "annular"
pi = 3.141592653979382
for i=0 to 200
j = (i/200)*2
v = SMOOTHSTEP((1+sin(j*pi*5))/2,.3,.7)*255
a = SETPROF(p$,i,v)
next i

This example feeds the portion of the sinewave formula that results in a sine wave of 0 to 1 to the SMOOTHSTEP() function, with edge parameters of .3 and .7. That produces a result of 0 below .3, 1 above .7, and a smoothly changing value between the two. This can help you avoid the harsh edges produced by the STEP() function if it is too fierce for you.

You'll find the names for all the system profiles located here.

Using CLAMP() to limit excursions

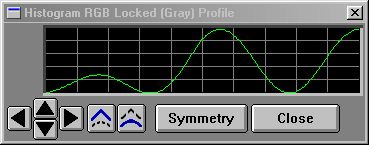REM makes sine wave cycles
c = 2.25
p$ = "histo"
pi = 3.141592653979382
for i=0 to 200
j = (i/200)*2
v = ((1+sin(j*pi*c))/2)*255
a = SETPROF(p$,i,v)
next i
return

REM rampulates from 0-1 by 1/2 profile distance
p$="histo"
for i=0 to 200
a=SETPROF(p$,i,GETPROF(p$,i)*CLAMP((i/200)*2,0,1))
next i
return

The example image above shows what happens if you call the subroutines at 200, then at 300.

The first subroutine produces a 2.25 cycle sine wave of full amplitude.

The second reads that back from the profile, then multiplies each profile value by a ramp that would go linearly from 0-2 over the length of the profile ((i/200)*2) except it was fed to CLAMP() with limits of 0 and 1. So what happens is that when the ramp hits 1, it stays there, period. So the sine wave goes from 0 to full amplitude from the begining to 1/2 the profile, and after that it just stays at full amplitude.

This example was taken from a metallic texture generating script that remaps linear brightness into a semblance of metallic reflections.

You'll find the names for all the system profiles located here.

F/x has a series of useful scripting functions you can use to control waveforms. They are:

CEIL()
FLOOR()
MIN()
MAX()
HILIM()
LOWLIM()
CLAMP()
STEP()
SMOOTHSTEP()
ABS()

If you want to be a profile wizard, you'll want to look into all of these!

Keyboard Navigation

, Previous Page . Next Page t TOC i Index o Operators g Glossary

Table of Contents Index Glossary Op Index Parent

WinImages F/x, Morph and all associated documentation
Copyright © 1992-2007 Black Belt Systems ALL RIGHTS RESERVED Under the Pan-American Conventions
WinImages F/x Manual Version 7, Revision 6, Level A

This manual was generated with wtfm wtfm uses aa_macro and SqLite aa_macro uses python 2.7 Page 277

box